Triangle Review: Fundamentals of Triangle , Formula’s for Triangle , Types of Triangle , 45° – 45° – 90° Triangle , 30° – 60° – 90° Triangle , Congruent Triangles, Similar Triangles
Class Questions: Practice Examples 1, Practice Examples 2
Practice Questions: Exercise 1, Exercise 2, Exercise 3 , Exercise 4
Q.16
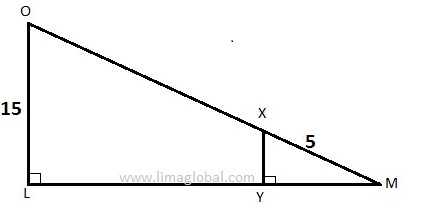
In the below figure OX = LY = 20, find YM ?
A. 5
B. 6
C. 10
D. 9
E. 4
Solution;
For Δ OLM and Δ XYM (i) angles ∠L = ∠Y and (ii) ∠M is common for both the triangles. Hence, Δ OLM and Δ XYM are similar triangles.
OL/XY = OM/XM ( OM = 20 + 5 = 25)
15/XY = 25 / 5
XY = 3
Now apply Pythagorean’s theorem to find YM.
YM² = XM² – XY²
= 25- 9
= 16
Taking square root both side
YM = 4
Correct answer choice is ‘E’.
Triangle Review: Fundamentals of Triangle , Formula’s for Triangle , Types of Triangle , 45° – 45° – 90° Triangle , 30° – 60° – 90° Triangle , Congruent Triangles, Similar Triangles
Class Questions: Practice Examples 1, Practice Examples 2
Practice Questions : Exercise 1, Exercise 2, Exercise 3 , Exercise 4