Geometry Exercise : Q.1 to Q.8 , Q. 9 to Q. 14
Answer 1
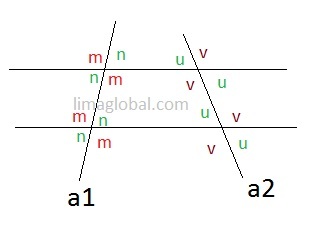
As in above figure always remember that opposite angles of a transversal line intersecting two parallel lines are always equal. Now this problem becomes quite easy for you.
For transversal line a1;
n = 57 °
So, n = x = 57°
For transversal line a2; u = 42
u + v = 180
v = 180 – 42
v = 138°
v = y = 138°
Answer 2
In the given figure two sides AC and BC are equal of a triangle that means it is an isosceles triangle. Hence Angle A = Angle B.
Angle A = 180 -125 = 55°
Therefor Angle B is also 55°
Addition of angles for any triangle = 180°
55 + 55 + x = 180°
x = 180 -110
x = 70°
y = 180 – Angle B
= 180 – 55
y = 125°
Answer 3
In the given figure; addition of angles of triangle
x + y + (180 – z ) = 180
x + y – z = 180 – 180
= 0
x + y = z
Answer 4
Decagon is 10 sided polygon
Use the formula ;
Sum of the measures of the interior angles of n – sided polygon
= ( n – 2 ) x 180
Here sides are 10, i.e. n =10
Hence, Sum of measures of interior angles of a Decagon is
= (10-2) x 180
= 8 x 180
= 1440°
Answer 5
If decagon is regular that means it will have all equal 10 sides and it will have 10 numbers of angles
n = Number of Sides
Number of angles = 10
Total measures of angles of decagon from question ‘4’ is 1440°, then measure of each angle = 1440/10
= 144°
Answer 6
It is given that the triangle is an isosceles triangle means two of the sides has to be equal. In the question measure of two sides are given , So the third side may be 15 or may be 22.
Perimeter of a triangle is a + b + c
- If we take that third side = 15 then perimeter of triangle is = 15 + 15 + 22 = 52.
- If we take that third side = 22 then perimeter of triangle is = 15 + 22 + 22 = 59.
Perimeter of triangle could be 52 or 59.
Answer 7.
Refer review section of this website limaglobal.com
Two triangles are similar
Answer 8.
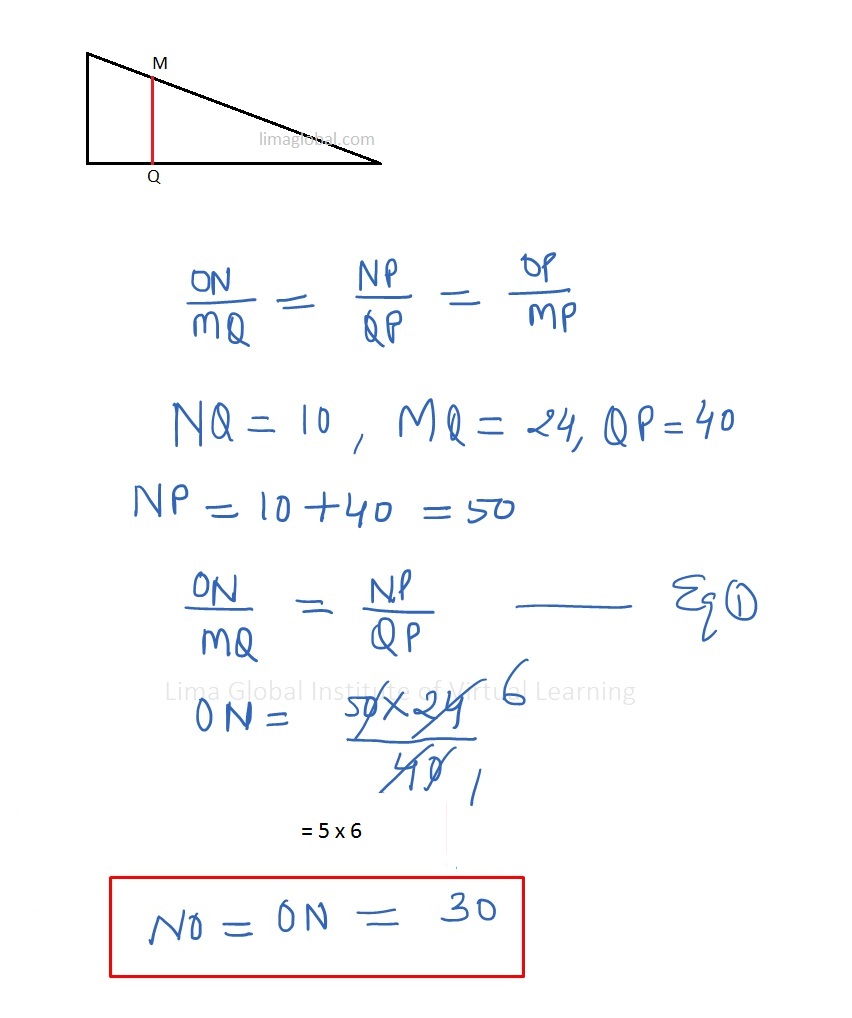
Refer the figure in the book;
Two triangles share the common vertex. Both are right angled triangle. The shape of both the triangles ONP and MQP are same of being right angled triangles but the sizes are different , So we can apply the formula for similar triangles;
In the similar triangles sides of one triangle is in same ratio to other triangle;
Now apply Pythagorean Theorem for Δ ONP
OP2 = NO2 + NP2
= 30 2 + 50 2
= 900 + 2500
= 3400
OP = 10 √34