Circles Review – Fundamentals of Circles, Formulas for Circle, Congruent Circles, Tangent to a circle, Polygon inscribed in a Circle , Circle inscribed in a circle, Concentric Circles
Class Questions – Exercise 1 Exercise 2 Exercise 3 Exercise 4 Exercise 5
Practice Questions – Solutions
–———————————————————————————————————
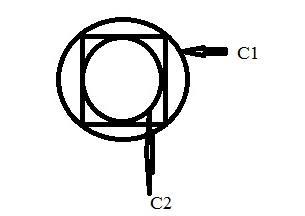
Q.1 In the following figure circle C1 circumscribed a square and again that square circumscribed another circle C2. What is ratio of the area of Circle C1 to Circle C2
A. π – 1
B. 2π
C. 4/√2
D. 4π – 3
E. 2
Solution:
If we draw some lines in the figure ; it will be as follows

Suppose radius of Circle C2 = PR = r
Area = π r2
Area of square = 2r x 2r = 4r2
To find Diagonal of triangle QPR apply Pythagorean Theorem
PQ2 = PR2 + QR2
= r2 + r2
= 2r2
PQ = r √2
Diagonal of triangle = Radius of Outer circle C1 = PS = PQ = r √2
Area of Circle C1 = π x (r √2)2
= π x r2 x 2
= 2 π r2
Now the ratio of Circle C1 to Circle C2 = 2 π r²/ π r2
= 2
So answer is E.
Q.2
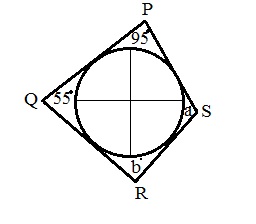
In the below figure a circle is inscribed in a Quadrilateral PQRS, then a + b =?
A. 200
B. 150
C. 125
D. 210
E. 305
Solution ;
Addition of angles of a quadrilateral = 360° . When any quadrilateral circumscribed a circle , then addition of its opposite angle should be 180°.
A + 55 = 180 , so a = 180 – 55 = 125
B + 95 = 180 so b = 180 – 95 = 85
Hence a + b = 125 + 85 = 210
Correct answer choice will be ‘D’.
Q.3
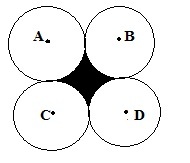
In the above figure four congruent circles having radius ‘a’ with center A, B, C and D are tangent to each other. Then what is the area of shaded region?
A. a2 (4 + π)
B. (4π – π)
C. 44 – a2
D. a2 (4 – π)
E. 16
Solution;
If we draw lines and join the center of circles we will get following figure;
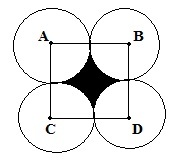
Now solving this problem become quite easy
Radius of each circle is ‘a’ so length of segment AB = CD = ’2a’ and segment AC = BD = ‘2a’
Area of square will be = length x length = 2a x 2a = 4a2
Area of each circle = π x a x a = π a2
Area of quarter of a circle = π a² / 4
Area of ‘4’ quarters = 4 x π a² / 4
= π a2
So area of shaded region = Area of square – Area occupied by quarters of circles
= 4a2 – π a2
= a2 (4 – π)
The correct answer choice is D.
Q.4
XY = AB = Diameter of circle with center O.
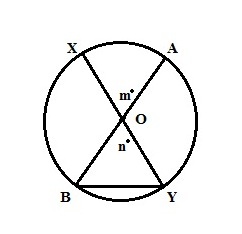
Quantity A Quantity B
m n
A. If Quantity A is greater
B. If Quantity B is greater
C. If Quantity A and Quantity B are equal
D. The relationship cannot be determined from given information
Solution
As the line segments XY and AB both are diameter of circle. The opposite angels will always be same at point of intersection ‘O’.
Angle XOA = Angle BOY, i.e. m = n.
So correct answer will be C.
Q. 5 If 12 hour ancient circular wall clock’s needle moves from 2 o’ clock to 5 o’ clock, then how much distance it will cover if radius of clock is equal to length of hour needle , which is 8.
A. 4π
B. 2π + 9
C. 69 +π2
D. (81 – 3) π2
E. 9π+7
Solution;
If we draw a figure as per given data it will look like this,

For each hour, needle will move 30°. When it will reach from 2 O’clock to 5 O’clock, it would have moved 90°. So Central angle of circle = 90°

The correct answer is A.
Q.6 In the below figure K is the center of Circle and vertex of a square is touching it from inside
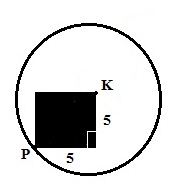
Quantity A Quantity B
Radius of Circle 25
A. If Quantity A is greater
B. If Quantity B is greater
C. If Quantity A and Quantity B are equal
D. The relationship cannot be determined from given information
Solution;
After joining we can see that Segments PK = KM = Radius of Circle= r
If we draw a line joining point P to point K
PK = Radius of Circle = r,
Using Pythagorean Theorem, we can easily find out
r2 = 52 + 52
= 25 + 25
= 50
= 25 x 2
Taking root both sides
r = 5√2
If we compare Quantity A with Quantity B the value of Quantity A will be greater .
So answer choice is A.
Q. 7 In the following figure L is center of circle;
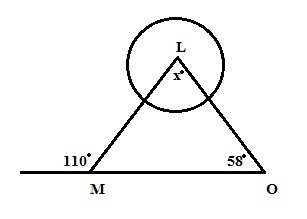
Quantity A Quantity B
x 55
A. If Quantity A is greater
B. If Quantity B is greater
C. If Quantity A and Quantity B are equal
D. The relationship cannot be determined from given information
Solution;
The addition of three sides of angle should be = 180°
Angle M = 180 – 110 = 70
Angle O =58
Angle L = x = 180 – (70 + 58) = 52
If we compare Quantity A which is = 52 and Quantity B = 55, Hence Quantity B will be larger than Quantity A,
The answer is B.
Q.8
In the above figure if DF = k, which is double the radius of each circle. ‘D’ and ‘F’ are center of circles respectively. Then what is the area of shaded region?
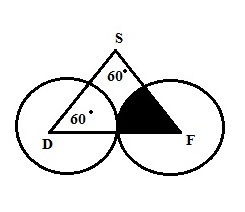
A. πk4
B. 4(-k)
C. πk²/4
D. ½ kπ2
E. π k²/ 24
Solution:

Hence correct answer Choice is E.
Q.9 Two circles each having diameters ‘j’ are inscribed in a rectangle PQRS.
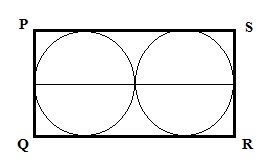
Quantity A Quantity B
Diagonal PR of rectangle 5 j
A. If Quantity A is greater
B. If Quantity B is greater
C. If Quantity A and Quantity B are equal
D. The relationship cannot be determined from given information
Solution;
Draw lines and join points P,R and Q,S
Apply Pythagorean Theorem to solve it further
QR = Diameter of one circle + Diameter of second circle = 2 x j
PQ = Diameter of circle = j
PR2 = PQ2 + QR2
= j2 + (2j)2
= j2 + 4j2
= 5j2
Taking square root both side
PR = j √5
Quantity A = Diagonal PR of rectangle = j√5 = √5 times of j
Quantity B = 5j = j5 = 5 times of j
If we compare both the quantity then Quantity B will be larger than Quantity A.
So the correct answer choice is B.
Q.10
An equilateral triangle with a perimeter 24 is inscribed in a circle. If radius of circle is equal to side of triangle then what is the perimeter of circle?
Solution;
Draw a sketch
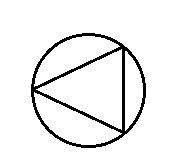
Equilateral triangle perimeter is 24 so each side will be = 24/3 = 8
Radius of circle = side of triangle = 8
So perimeter of circle = 2 x π x r
= 2 x π x 8
= 16π
Correct answer is A.













