Sets Review: Review , Types of Sets , Intersection of sets , Union of sets, Venn Diagram , Inclusion Exclusion Principle
Class Questions : Exercise 1 Exercise 2 Exercise 3 Exercise 4 Exercise 5
Practice Questions : Solutions
_________________________________________________________________
Sets
A ‘Set’ is collection of things or objects with some property. Like numbers of student in class, types of fruits in a shopping mall, women in a group wearing Swiss Watch, language books in a library-etc.
It is denoted by curly brackets { }. The objects in the sets are called its elements. The elements are separated by commas.
Example:
Student of class 5th = Set P
Students are John, Jolly, Elian, Barbie and Nelson. All students will be identified as elements of Set ‘P’.
So, Set P = {John, Jolly, Elian, Barbie, Nelson}
Types of Sets
1. Finite Set
A set with finite number of elements is called as Finite Set. In simple words, we can count the elements in a set.
Like set A of multiple of 3 is;
A = {6, 9, 12, 15, 18}
2. Infinite Set
A set with infinite number of elements called an Infinite set. Here there is no limit to elements of set. We cannot count it.
Like Set of stars in the sky, Set of all integers etc.
3. Empty Set
A set with no member is called as Empty set and is denoted by symbol “Ø”.
4. Subset
If P and Q are two sets and all the elements of set Q are same as of set P, then Set Q is a subset of Set P.
Example;
A = {1, 2, 3, 4, 7, 9}
B = {2, 3}
As elements of Set B, 2 and 3 are elements of Set A also, Set B is a subset of Set A.
“Each element is a subset of its own set”.
-
{1}, {2}, {3}, {4},{7}, {9} are subset of Set A.
Note: Ø is a subset of every set.
5. Universal Set
A universal set is a collection of all the objects under consideration. It is denoted by capital letter ‘U’. In Venn diagram it is being represented in the rectangular shape. All the other sets are subsets of Universal set.
Example;
U = { 3,6,9,12,15,18,21,24,27}
X= {6, 9, 12}
Y = {21, 27}
Intersection of Sets
If A and B are two sets, then Set of all the elements which are common in both Sets A and B will be called as Intersection of Sets. It is denoted by symbol A ∩ B.
Example;
Suppose there are two sets X & Y. ‘X’ represents students in music class while ‘Y’ represents students in dance class.
Set X = {Allen, Julia, Nick, John, Mary, Maria}
Set Y = {Robert, John, Maria, Victoria, Rita, Nancy}
Here, in the above two sets X & Y common elements are John and Maria. So if we represent intersection of Set X and Set Y as Set C then,
Set C = X ∩ Y
Set C = X ∩ Y = {John, Maria}
Union of Sets
If A and B are two sets, then set of all the elements of Set A and Set B taken together is called as Union of Sets. It is denoted by A ∪ B.
If we continue with above example then,
A ∪ B = {Allen, Julia, Nick, John, Mary, Maria, Robert, Victoria, Rita, Nancy}
Venn Diagram
We can represent Intersection of sets and Union of sets with circular diagrams. These diagrams are known as Venn diagram. If elements of sets are common then circular regions overlap each other, but if there are no common elements among the sets then circular diagram shown individually presenting each set.
Inclusion Exclusion Principle:
It states that number of elements in union of two sets is equal to the sum of their individual number of elements minus the number of elements in their intersection.
If P and Q are two sets then,
P ∪ Q = P + Q – (P ∩ Q)
-
Where P ∩ Q is a subset of both sets P and Q, so it has to be deducted to avoid double counting of elements.
Example;
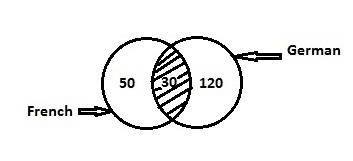
In a language class 50 students are learning French, 120 students are learning German, and of these 30 students learning both the languages.
Quantity A Quantity B
Total students in both the Class 140
A. Quantity A is greater
B. Quantity B is greater
C. Quantity A and B are equal
D. Relationship cannot be defined from given information
Solution:
Let us draw a Venn diagram for this
Consider students in French Class as Set F and students in German class as Set G.
Total number of students in both the class = F + G = F ∪ G, but 30 students have joined both the classes.
So applying the formula;
P ∪ Q = P + Q – (P ∩ Q)
F ∪ G = F + G – (F ∩ G)
= 50 + 120 – (30)
= 140
The value for total number of students is 140.
Now for Quantity B the value is = 140.
If we compare Quantity A and Quantity B, both are equal.
Correct answer choice is “C”.
Example;
Draw Venn diagram for following sets.
U is universal set = { 2,4,6,8,10,12,16,18,20,22,24,26,28,30}
-
P = {all positive even integers below 20}
-
Q = {multiple of 2 between 10 to 20}
-
R = {2,4,6,20,22,24}
Solution;
As the universal set is given so all the elements of P, Q and R will be selected from it.
U = { 2,4,6,8,10,12,14,16,18,20,22,24,26,28,30}
-
P = {2,4,6,8,10,12,14 }
-
Q = {12,14,16,18 }
-
R = {2,4,6,20,22,24}
We can see that Set P and Set Q are having common elements, Set P and Set R are having common elements but there are no common elements among Set Q and Set R.
In the above Venn diagram Rectangle shows Universal Set ‘U’. Three circles represent sets P, Q and R respectively.
-
Elements 12 and 14 are common to Set P and Set Q, shown with shaded region among Circle P and Circle Q.
-
There is no element which is common in Set Q and Set R.
-
Elements 2, 4, and 6 are common among Set P and Set R.
-
The remaining elements which do not fall in any of the set are shown in the rectangle which represents Universal Set.