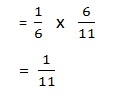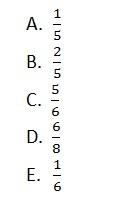#Probability Review: Mutually Exclusive Events , Independent Events , Dependent Events , Conditional Probability , Subtraction Rule , Addition Rule , Multiplication Rule
Practice Examples : Exercise 1 Exercise 2
Exercise Questions : Solutions
_____________________________________________________________________________________________________
Q.1
A box contains 6 yellow balloons, 3 blue balloons, 2 green balloons and 1 pink balloon. Jennifer is going to pick 2 balloons at random without replacing from the box. What is the probability that the first balloon she picked will be green and the second will be yellow?
Solution
After reading the question it is understood that we need to find the probability of picking first green balloon and second yellow balloon. It is also clear that second event is dependent on first event as there is no replacement of first balloon so number of available choices will be changed for second balloon.
Event M = Picking first balloon
Event N = Picking second balloon
The probability that first balloon picked is green = P (M) =2/12 =1/6
If the first balloon selected is green then the choices for next selection is 6 yellow , 3 blue, 1 green and 1 pink left in the box with a total of 11 as first balloon is not replaced .
Probability of picking second yellow balloon = P (N) =6/11
The probability that second balloon picked will be yellow, given that first balloon picked is green = P (N) = 6/11 .
So, the probability for first green balloon and second yellow balloon without replacement of first green balloon = P (M) x P (N)
Hint: Conditional Probability with dependent events.
The correct answer choice is B.
Q.2
Albert tossed a dice. What is the probability that it will land on 3?
Solution;
After tossing a dice there is only 6 possible outcomes.
Event M = 1, 2,3,4,5 or 6. Each number is likely to occur in tossing a dice once.
So probability of the event M that dice will land on 3 is
Correct answer choice is E.
Q.3
One box is having y number chalks of red and green colors in equal quantity. A chalk is taken away randomly from the box. What is the probability that the chalk will be red or green?
A. 1.0
B . 0.8
C. 0.5
D. 0.6
E. 0.75
Solution;
Here both events are mutually exclusive means if the chalk picked is red then it cannot be green and if the picked chalk is green then it cannot be red.
So,
P (M) and P (N) = 0
Event M = Chalk is red
Event N = Chalk is green
There are total y chalks of red and green color in equal quantity that means there will be y/2 red chalks and y/2 green chalks.
Suppose y = 100 then red chalks = 50, green chalks = 50
P (M) = 50/100 = 1/2
P (N) = 50/100 = 1/2
P (M∪N) = P (M or N) = P (M) + P (N)
P (M∪ N) = 1/2 + 1/2
= 1
The correct answer choice is A.
Q.4
What is the probability of rolling two six sided dice and getting 3 at least one of them?
A. 1/11
B. 23/11
C. 11/36
D. 5/6
E. 5/11
Solution;
Getting 3 At least one of the dice, means let us take that we have not get 3 in any trial.
Probability of getting 3 once after rolling one dice = 1/6
Probability of not getting 3 after rolling dice once = 1 – 1/6
= 5/6
Here two dice are rolled
Event M = first dice rolled
Event N = second dice rolled
Event M and N are independent events. So probability of not getting 3 after rolling two dice
P (M and N) = P (M) x P (N)
= 5/6 x 5/6
= 25/36
Probability of getting 3 at least one of the roll for two dice
= 1 – Probability of not getting 3
= 1 – 25/36
= 11/36
Correct answer choice is C.
Q.5
In a basket there are 7 green and 5 yellow fruits. Sheila takes away two fruits at random with replacement from basket. What is the probability that both fruits are green?
Solution;
Event M = First fruit is green.
Event N = Second fruit is green.
Total there are 12 fruits.
P (M) =
After taking away one fruit it is being replaced again so there will be still total 12 fruits, so both the events are independent.
Hence, P (N) =
Probability of Event M and Event N
P (M∩N) = P (M and N) = P (M) x P (N)
P (M∩N) = 7/12 x 7/12
= 49/144
= 0.34
The answer is 0.34.
Q.6
What is the probability, if after tossing a dice it lands on even number which is lesser than 5?
A. 1.0
B. 1/4
C. 1/6
D. 1/3
E. 2/5
Solution;
In a dice there are two even numbers 2 & 4 which are lesser then 5.
So, for rolling a dice once, probability of an even number which is lesser then 5 is;
P (M) = 2/6 = 1/3
Correct answer choice is D.
Q.7
From a deck of 52 playing cards, Leena has drawn one card randomly. She will win a luxury car if the card is diamond or a king. What is the probability that she will win the game?
A. 1/13
B. 4/13
C. 6/13
D. 5/52
E. 2/13
Solution;
As we all know that in a deck there are 52 cards with 13 diamonds and 4 kings.
Event M = Card is a diamond
P (M) = 13/52
Event N = Card is a king
P (N) = 4/52
But in diamonds there will be also a king, so P (M∩N) = 1/52
When Leena draws a card randomly;
It can be diamond
Or
It can be a king
In both the possibility she will win luxury car
Applying addition formula
P (M∪N) = P (M) + P (N) – P (M∩N)
P (M∪N) = 13/52 + 4/52 – 1/52
= 16/52
= 4/13
So, correct answer choice is B.
Q.8
If the probability for the events M, N, and O is P (M) =0.11, P (N) = 0.28 and P (O) = 0.64. The events M, N and O are mutually exclusive events.
Quantity A Quantity B
P (M and N) zero
A. If Quantity A is greater
B. If Quantity B is greater
C. If Quantity A and Quantity B are equal
D. The relationship cannot be determined from given information
Solution;
In the above problem the probability of three events individually given and events M, N and event O are mutually exclusive. So the probability of
P (M and N) = 0
If we compare quantity A with quantity B, the value for both is equal. So, correct answer choice is C.
Q.9
What is the probability of rolling a 24 sided dice once and getting multiple of 8 or an even number lesser than 20?
Solution;
Event M = after rolling 24 sided dice once, chances of getting the multiple of 8 will be = 8, 16, 24.
P (M) = 3/24
Event N = Getting even number lesser then 20 will be
2, 4, 6, 8, 10, 12, 14, 16 and 18
P (N) = 10/24
Here the numbers 8, 16 are multiple of 8 and even also.
P (M and N) = 2/24
So, probability of getting 8 or an even number lesser than 20 is;
P (M) + P (N) – P (M and N) = 3/24 + 10/24 – 2/24
= 11/24
Correct answer is B.
Q.10
In a building there are 10 flats, John knocked randomly at a door of one of the flats. What is the probability that he knocked the door of fifth flat or door of a flat which is at odd number in the building?
A. 1/10
B. 1/15
C. 1/20
D. 25
E. 1/35
Solution;
Event M = He knocked at a door of 5th flat
P (M) = 1/10
Event N = He knocked at a door of the flat which is at odd number
Flats at odd number are 1,3,5,7 and 9.
P (N) = 5/10
Here two events M and N are dependent. They both occur, because fifth flat is at odd number itself so as given in the review section for conditional probability multiply the probability of event M with probability of N given that event M already occurred.
P (M) P (N) = 1/10 X 5/10
= 1/20
So correct answer choice is C.