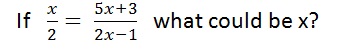Practice Examples 1 , Practice Examples 2
limaglobal.com
[embedyt] http://www.youtube.com/watch?v=MDQVG6-eVh0[/embedyt]
Q.1
A. 7
B. 8
C. -5
D. -2
E. 3
Solution;
( x+1)x = -2 x (x-5)
x2 + x = -2x + 10
x2 + x + 2x -10 = 0
x2 + 3x – 10 = 0
x2 + 5x – 2x – 10 = 0
x(x+5) -2(x+5) =0
(x+5) (x-2) = 0
Product of factors will be zero only when;
x+ 5 = 0 or x-2 = 0
x =-5 or x = 2
Maximum value of x = 2 and minimum value of x = -5
Difference between the two values is =2 – (- 5)
= 2 + 5
= 7
The answer is ‘A’.
limaglobal.com
Q.2
A. x > 7
B. x =5
C. -1 < x < 0
D. 1<x<2
E. Cannot determine
Solution;
x(2x-1) = 2(5x+3)
2x2 – x = 10x+6
2x2 – x -10 x -6 = 0
2x2 – 11x – 6 = 0
2x2 – 12 x + x – 6 = 0
2x(x-6) + 1 (x-6) = 0
(x-6) (2x +1) = 0
(x-6) = 0 or (2x+1) = 0
x = 6 or x = -1/2
We are getting two values for ‘x’. If we look at the answer choices
- For A; x > 7 , not possible for both values of ‘x’, this is not the answer.
- For B; x =5 , Not satisfy the equation
- For C; -1 < x < 0 , Here the value of x is between – 1 and 0 which satisfy one of the value of x which is -1/2.
- For D; 1<x<2 , the value of x is between 1 and 2 which is not correct
- For E; Not valid statement
As per the answer choices given only ‘C’ satisfy the value -1/2 of x. The other value 6 is not given in the choices.
Hence, the correct answer is ‘C’.
Q.3
If x2 – 8x -20 = 0
Quantity A Quantity B
Maximum value of x 11
A. If Quantity A is greater
B. If Quantity B is greater
C. If Quantity A and Quantity B are equal
D. The relationship cannot be determined from given information
Solution;
x2 – 8x -20 = 0
x2 – 10x + 2x – 20 = 0
x(x – 10) + 2 (x-10) = 0
(x-10) (x+2) = 0
(x-10) = 0 or (x +2) = 0
x = 10 or x = -2
The maximum value of x is 10 which is lesser than 11 so Quantity B is greater.
The correct answer is B.
Q.4
x2 + 1 = 26
Quantity A Quantity B
x 5
A. If Quantity A is greater
B. If Quantity B is greater
C. If Quantity A and Quantity B are equal
D. The relationship cannot be determined from given information
Solution;
x2 + 1 = 26
x2 + 1 – 26 = 0
x2 – 25 = 0
x2 – 5² = 0
(x – 5) (x + 5) = 0
x = 5 or x = -5
Let us compare the quantity A with B;
- When x = 5 Quantity A and quantity B are equal , the answer is ‘C’
- When x =-5 Quantity B is greater, the answer is ‘B’
Thus, the correct answer is ‘D’, as we cannot reach any conclusion with the given data.
Review of Quadratic Equations More Practice Examples on quadratic Equation
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>NEXT PAGE
