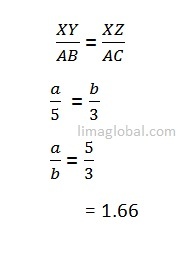#Geometry
Triangle
Triangle Review: Fundamentals of Triangle , Formula’s for Triangle , Types of Triangle , 45° – 45° – 90° Triangle , 30° – 60° – 90° Triangle , Congruent Triangles, Similar Triangles
Class Questions : Practice Examples 1, Practice Examples 2
Practice Questions : Exercise 1, Exercise 2, Exercise 3 , Exercise 4
Q.6 www.limaglobal.com
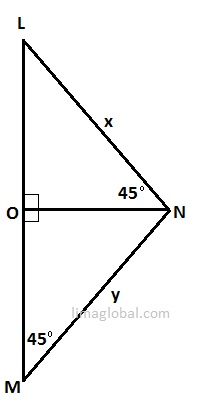
Refer below figure
Quantity A Quantity B
x y
A. If Quantity A is greater
B. If Quantity B is greater
C. If Quantity A and Quantity B are equal
D. The relationship cannot be determined from given information
Solution;
In Δ LON ∠O = 90°, ∠ N = 45°, so ∠ L = 180° – 90° – 45° = 45°
In Δ OMN ∠ O = 90° m = 45°, so ∠N = 180° – 90° – 45° = 45°
Now applying the rule for 45° – 45° – 90° triangle; the length of sides of the triangle will be in the ratio of 1: 1: √2.
If ON = LO = a, then LN = x = √2 a
Similarly ON = OM = a, then MN = y = √2a
So if we compare Quantity A with Quantity B the value is same.
The correct answer choice will be ‘C’.
Q.7 www.limaglobal.com
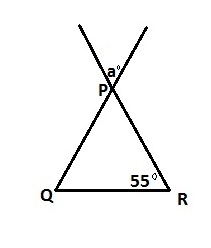
In the above figure PQ = PR. Then what is the value of a?
A. 65
B. 55
C. 80
D. 70
E. 60
Solution;
PQ = PR, so Δ PQR is an isosceles triangle. Hence ∠R = ∠Q = 55°
∠P = 180° – 55° – 55° = 180° – 110° = 70°.
As the rule for lines opposite angles of intersecting lines remains same so, a° = 70°.
The correct answer choice is ‘D’.
Lima Global Institute of Virtual Learning
Q.8 www.limaglobal.com
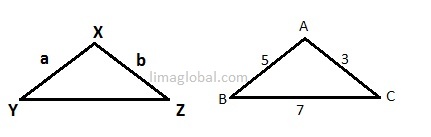
In the below figure XYZ and ABC are similar triangles.
Quantity A Quantity B
5/6 a/b
A. If Quantity A is greater
B. If Quantity B is greater
C. If Quantity A and Quantity B are equal
D. The relationship cannot be determined from given information
Solution;
For XYZ and ABC to be similar triangles all the sides of two triangles should be proportionate.
Now if we compare Quantity A which is = 0.83 and Quantity B which is = 1.66, so Quantity B will always be greater.
The correct answer choice is ‘B’.
Q.9 www.limaglobal.com
What could be the maximum possible length of the hypotenuse of a right triangle with sides 3 and 4? If the length of the hypotenuse is an integer.
A. 5
B. 6
C. 4
D. 3
E. 7
Solution;
When we find third side it should be maximum when it is lesser than addition of the other two sides which is = 3 + 4 = 7 as, it should be integer means maximum length of third side could be 1 less than 7
i.e. = 6.
In this type of problems, there is a catch. Here it is clearly given that it is a right triangle so the length of hypotenuse needs to be calculated using Pythagorean Theorem, and length of third side cannot be larger or lesser than that.
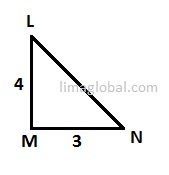
Let us understand this by following figure;
Length of hypotenuse “LN” for triangle Δ LMN
LN2 = LM2 + MN2
= 42 + 32
= 16 + 9
= 25
LN = 5
So correct answer choice is ‘A’.
Q.10 www.limaglobal.com
What is the area of two congruent triangles with the base as double to its height? Take height as ‘h’.
A. 2h
B. 4h2
C. 4h
D. 6
E. 2h2
Solution;
Area of triangle = 1/2 x base x height
= 1/2 x 2h x h
= h2
Area of two congruent triangles = 2 x h2
= 2h2
Correct answer choice is ‘E’.
<<<<<<<<<<<<<<<<<<<<<PREVIOUS PAGE
Triangle
Triangle Review: Fundamentals of Triangle , Formula’s for Triangle , Types of Triangle , 45° – 45° – 90° Triangle , 30° – 60° – 90° Triangle , Congruent Triangles, Similar Triangles
Class Questions : Practice Examples 1, Practice Examples 2
Practice Questions : Exercise 1, Exercise 2, Exercise 3 , Exercise 4