Q.1
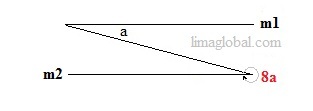
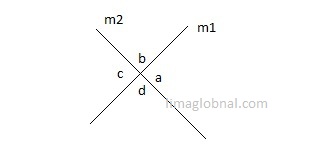
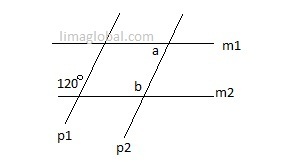
Line m1 is parallel to line m2 then what is the value of a – 5 ?
A . 50
B. 35
C. 25
D. 20
E. 15
Solution:
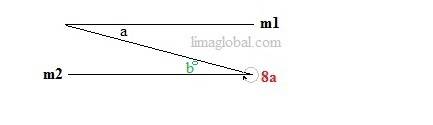
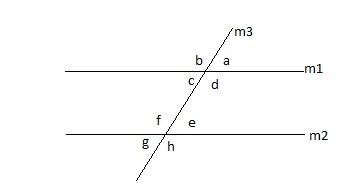
In parallel lines alternate interior opposite angles are same so if we take angle ‘b’ at line ‘m2’ with the intersecting line then
b + 8a = 360°
As lines m1 and m2 are parallel; b and a are alternate interior angles, so b = a
a + 8a = 360
9a = 360
a = 360/9
a = 40°
So, a – 5 = 40° – 5° = 35°
Correct Answer is ‘B’
Q.2
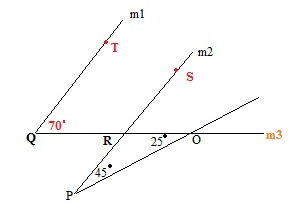
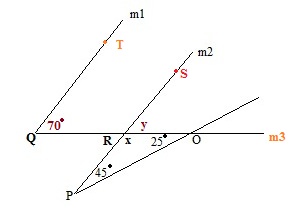
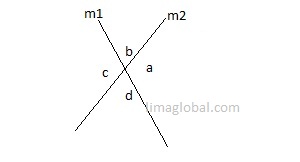
Refer the following figure, which of the following statement is true?
I. line m1 is parallel to line m2
II. line m1 is not parallel to line m2
A. Only statement I is true
B. Only statement II is true
C. None of the statement is true
Solution ;
Here we need to find out whether line m1 is parallel to m2 or not
As per the conditions for two lines to be parallel, the corresponding angles of parallel lines should be same with the transversal line.
In triangle ORP let us take ∠ ORP = x° , ∠ ORS = y°
So, x + 25° + 45° = 180°
x = 180° – 70°
x = 110°
∠ ORP + ∠ ORS should be = 180°
x + y = 180°
110 + y = 180°
y = 180° – 110°
y = 70°
∠ OQT and ∠ORS are corresponding angles with the transversal line m3
∠ OQT = ∠ ORS = 70°
Hence statement I is true , correct answer is ‘A’.
Q.3
Line m1 is parallel to m2 and b =65° .
Quantity A Quantity B
Measure of ‘h’ 65°
A. Quantity A is greater
B. Quantity B is greater
C. Quantity A and Quantity B are equal
D. The relationship cannot be determined
Answer
As line m1 is parallel to m2 then alternate exterior angles are congruent . Here ‘b’ and ‘h’ are alternate exterior angles ,so if ‘b’ = 65 then h =65 .
Quantity A is equal to Quantity B ,
Correct answer choice is ‘C’.
Q.4
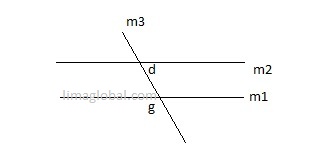
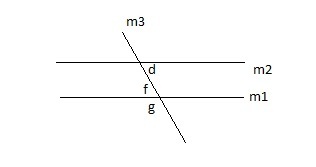
If m1 ǀǀ m2 and d = 75° , what is the value of g?
A. 100
B. 102
C. 110
D. 90
E. 105
Answer :
Let us mark angle ‘f’
Here d and f are alternate interior angles so both are congruent , if d = 75° then f will be 75°.
f+g = 180
75 + g = 180
g = 180 -75
g = 105°
Correct answer is ‘E’
Q.5
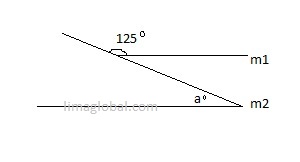
In the below figure a = 125° .
Quantity A Quantity B
125 b + d
A. Quantity A is greater
B. Quantity B is greater
C. Quantity A and Quantity B are equal
D. The relationship cannot be determined
Answer
Line m1 intersect m2, a +b = 180°
b = 180 – 125
b = 55°
‘b’ and ‘d’ are vertically opposite angles so both are congruent b = d = 55°.
b+ d = 55 + 55 = 110°
If we compare Quantity A with Quantity B , Quantity A is greater ,
So, correct answer is ‘A’.
Q.6
In the above figure line m1 intersect line m2 , if ‘a’ = 2b then what is a+b +c?
A. 100°
B. 200°
C. 300°
D. 290°
E. 320°
Answer
Line m1 intersect line m2 , so all vertical angles are add up to 360°.
a + b+ c + d = 360°
a= 2b given and c + d (linear axiom) = 180°.
2b + b + 180 = 360°
3b = 180°
b = 180/3
b = 60°
a = 2b = 2 x 60 = 120°
a and c are vertical opposite angles so both are congruent ;
a = c = 120°
a + b + c = 120 + 60 + 120 = 300°
Correct answer choice is ‘C’.
Q.7
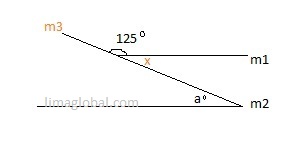
In the below figure m1 ǀǀ m2
Quantity A Quantity B
a +10 65°
A. Quantity A is greater
B. Quantity B is greater
C. Quantity A and Quantity B are equal
D. The relationship cannot be determined
Answer
Line m1 is parallel to m2 and if we give some more notations to the figure then it will be easy to solve
In the figure, line m3 is a transversal line which intersects lines m1 and m2.
From the figure x + 125° = 180°
x = 180 – 125 = 55°
x = 55 °
‘x’ and ‘a’ are alternate interior angles so both will be congruent, hence x = a = 55°
a + 10 = 55 + 10 = 65°
Now, if we compare quantity A with Quantity B, Both the quantities are equal ,
correct answer will be ‘C’.
Q.8
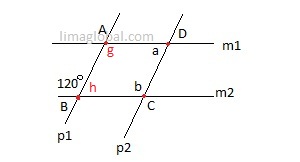
Refer the above figure ; m1 ǀǀ m2 , p1 ǀǀ p2
Quantity A Quantity B
a+b 185°
A. Quantity A is greater
B. Quantity B is greater
C. Quantity A and Quantity B are equal
D. The relationship cannot be determined
Answer
Let us add some more notations in the figure
Now, it is very clear that ABCD is a parallelogram addition of all the angle of a parallelogram is 360°.
a + b + g + h = 360°
h = 180 -120 = 60°
‘g’ is alternate interior angle to 120° , as both should be congruent ‘g’ = 120°
a +b + 120 + 60 = 360°
a + b = 360° – 180°
a+ b = 180°
If we compare Quantity A with Quantity B , Quantity B is greater ,
The answer is ‘B’.
Q.9
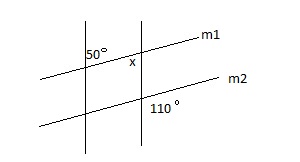
Refer the below figure ; m1 ǀǀ m2
What is the value of ‘x’?
A. 75
B. 65
C. 72
D. 85
E. 70
Answer
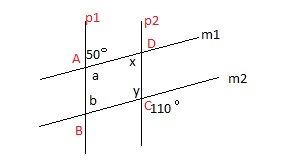
Add some notations to the figure
a = 180 – 50 = 130°
‘b’ is alternate interior angle so it will be 50° ( Refer Review section-Lines and Angles)
‘y’ is vertical angle , it will be equal to 110°.
ABCD is a parallelogram
a + b + x +y = 360°
130 + 50 + x + 110 = 360
x = 360 – 240
x = 70°
The answer is ‘E’.
Q.10
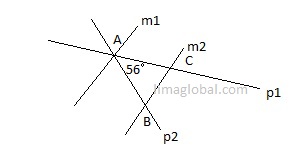
In the below figure AB = AC and line m1 ǀǀ m2.
Quantity A Quantity B
Angle B 63°
A. Quantity A is greater
B. Quantity B is greater
C. Quantity A and Quantity B are equal
D. The relationship cannot be determined
Answer
As it is given that AB = AC and enclosed figure is triangle so it is an isosceles triangle and in isosceles triangles, angles opposite to equals sides are same .
Addition of all three angles of a triangle = 180°
56 + a + a = 180
2a = 180 – 56
2a = 124
a = 62°
So, Angle B = 62°
After comparing Quantity A with Quantity B, Quantity B is greater than Quantity A.
The answer is ‘B’.