Practice Examples
Point – A point is a geometrical figure with no size and dimension.
Plane – We can imagine Plane as a geometrical figure with length and breadth extended infinitely in all directions with no thickness.
A line is a geometrical figure passes through minimum or at least two points and extends in any direction endlessly.
The portion of the line between two points of a line is known as line segment and the points are known as end points.
Mid-Point – Mid point is a point which divides the line segment into two equal parts or segments. Like in above figure M is a point so, AM = MB. These segments also known Congruent Line segments.
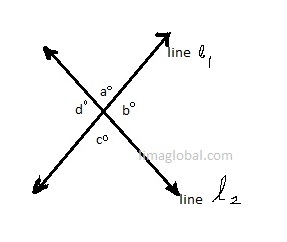
Intersection of Lines
When two lines intersect with each other they make intermediate angles a°, b °, c°, d°.
a° and c° , b° and d° are opposite angles and have equal measures. a° = c° and b° = d° . Opposite angles also called as vertical angles. a + b + c + d = 360° .
As the opposite angles are equal , it also identifies as congruent angles.
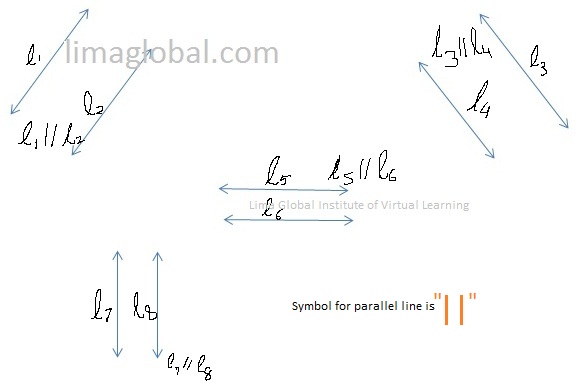
Parallel lines – When two lines do not intersect each other and moves endlessly in any direction with same slope then those lines are known as Parallel Lines. The angle of intersection is 0° between two lines.
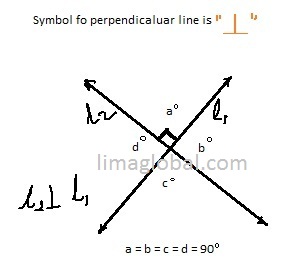
Perpendicular Lines – When two lines intersecting at 90° and moves endlessly are being called as perpendicular lines. Here both the lines make 4 ( four ) congruent angles of 90° each. When two lines form 90 angle generally defined as right angles.
Types of Angle
- Acute Angle – The angle lesser than the 90° is known as Acute Angle.
- Right Angle – The angle equal to 90° is known as Right Angle
- Obtuse Angle – The angle greater than 90° and less than 180 is Obtuse Angle.
- Straight Angle – The angle equal to 180° is a straight angle.
- Complementary Angle- When the addition of two angles are 90°, then those two angles are known as Complementary Angles.
- Supplementary Angle -When the addition of two angles are 180°, then those two angles are known as Supplementary Angles.
Terminology of angles and lines
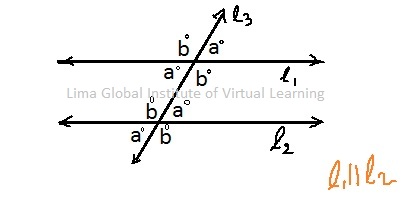
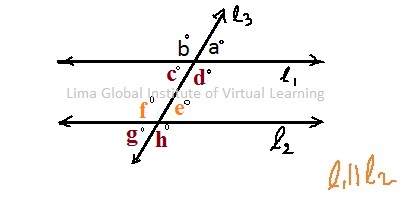
When there are two parallel lines and third line intersect those two lines, that time eight angles are formed.
- a + b = 180°
- a + b + a + b = 360°
- Opposite angles are always same for intersecting lines
Conditions to prove two lines to be parallel:
When transversal line ‘l3’ intersect two parallel lines ‘l1’ and ‘l2’ in the same plane then corresponding angles are congruent.
- a + b = 180° ; g + h = 180
- a + b + c + d = 360° , and e + f+ g + h = 360°
- Corresponding angles ; a = e , b = f , c = g , d = h
- Alternate Interior Angles ; d = f , c = e
- Alternate Exterior Angles ; b = h , a = g
- Consecutive Interior Angles; c + f = 180° , d + e = 180°
If any one of the four conditions satisfy, then two line are parallel.
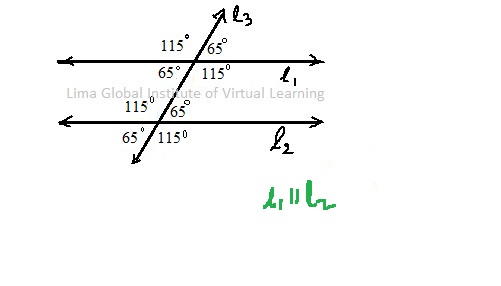
Example