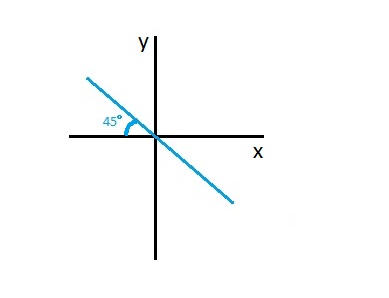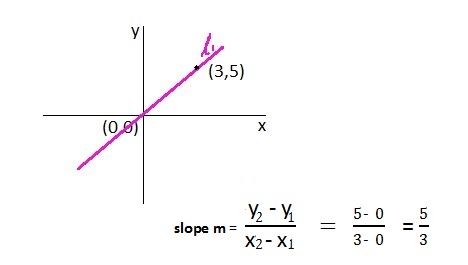Types of Slope
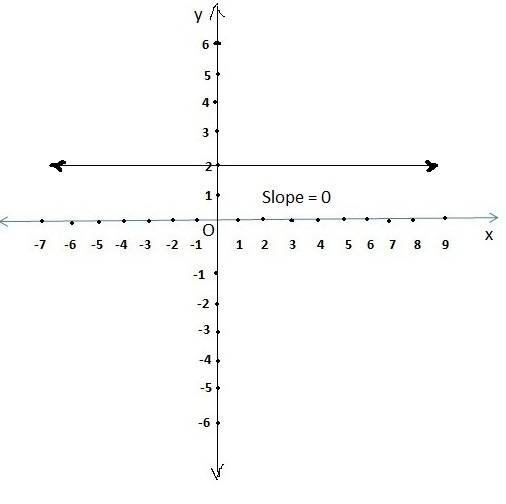
- For a horizontal line slope ‘ m’ = 0 , as rise is 0 we will get a equation in form as y = b. where b is the y intercept.
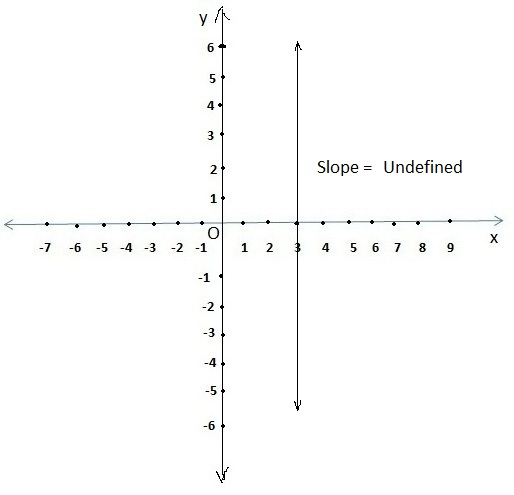
- For a vertical line slope ‘m’ = undefined , as run is 0 we will get a equation for vertical line is in form of x = a, where a is the x-intercept.
3. Two lines are parallel if their slopes are equal i.e. m1 = m2 that means if first line moves some distance horizontaly or vertically the second line will also move with same distace in x and y direction.
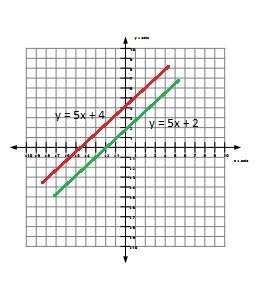
y = 5x + 4 ………………………………Equation (1)
y = 5x + 2 …………………………….Equation (2)
In the above equations of lines the slope of first line and the second line is same, which is = 5
So, m1 = m2 = 5
4. Two lines are perpendicular if their slopes are negative reciprocal to each other, i.e. m1 = – 1/m2
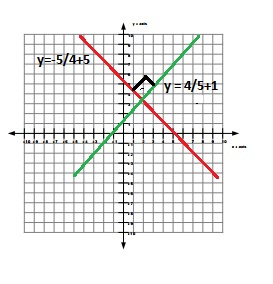
y = 4/5 +1 …………Equation (1)
y = – 5/4 +5 ……….Equation (2)
Here, both lines intersects each other at 90 or perpendicular to each other. In the above equation slope of first line m1 = 4/5 , slope of the second line m2 = -5/4 .
-5/4 is negative reciprocal to 4/5
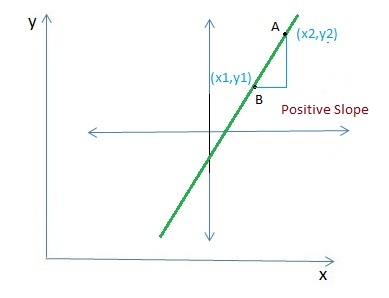
- Positive Slope – If the line passing through twopoints goes upwards from left to right , the slope will be positive. In this case slope ‘m’ > 0 always.
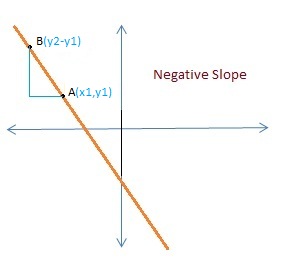
- Negative Slope – If the line passing through two points goes downwards from left to right will have negative slope. In this case slope ‘m’ < 0 always.
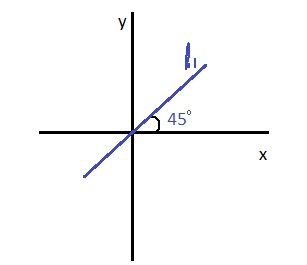
- If the slope ‘m’ = 1, then line is at 45° to x-axis in positive direction. It will be rising line.
- If the slope ‘m’ = – 1 then line is at 45° to x-axis in negative direction. It will be be a falling line.
- To find slope, two points are sufficient and out of that one point can be origin (0,0)