Linear Inequalities Review: Review, Compound Inequalities
Class Questions : Exercise 1 Exercise 2 Exercise 3 Exercise 4 Exercise 5
Practice Questions : Solutions
_____________________________________________________________________
Linear Inequalities
An algebraic linear expression with following notations is known as Linear Inequalities.
- > greater than
- < less than
- ≤ less than or equal to
- ≥ greater than or equal to
In linear inequalities we find all the values which justify the variable for given equation like;
So there are more than one solutions of an equation which we denote as set of solutions of an inequality, also identifies as Solution Set.
Equivalent Inequalities
Inequalities which are having same solution set are known as Equivalent Inequalities.
Rules for Linear Inequalities
- The direction of an inequality does not change if same constant is added or subtracted from both sides.
- The direction of an inequality does not change if same positive nonzero constant is multiplied or divided to both sides.
- The direction of inequality will be reversed or changed if same negative nonzero constant is multiplied or divided to both sides of an inequality.
- An inequality cannot be divided or multiplied by a variable.
Example
Let us check with this equation.
2 > 1
If we multiply both sides by -1 then -2 > -1, which is incorrect that time sign has to be reversed to get correct inequality.
So proper way of writing this equation is -2 < -1
Compound Inequalities
Two inequalities are connected with the word ‘and’ or ‘or’ is called as Compound Inequalities. In ‘and’ inequality we will consider the intersection of solution set, while for ‘or’ we need to consider union of solution set.
Like 3 < m < 8, -1 > m ≥ -3, -5 < n ≤ 7
- 3 < m < 8 can also be written as
- -1 > m ≥ -3 can also be written as
- -5 < n ≤ 7 can also be written as
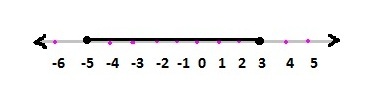
Let us take following example to understand ‘and’ inequality.
Example
a > -5 and a < 3
If we show this on a number line
We can understand that minimum value of is -5 and maximum value of is 3 means falls between -5 and 3. So, with ‘and’ inequality we get the range of a variable.
With following example we will learn about ‘or’ inequality.
Example
a > 3 or a <-1
The meaning of this inequality is that solution for all the values of
, where a is greater than 3 or a is less than -1.
Let us understand with number line
Above pink line shows all the values of greater than 3 and green line shows all the values of lesser than -1. So the parts between and including points -1 and 3 are not the solution to this inequality.
When an inequality is not connected with the word ‘and’ or ‘or’ it has to be considered as ‘and’ inequality where solution set is the intersection of both the inequalities.
As for example
-1 < x < 2, so it has to be an ‘and’ inequality because it can be written as
x > -1 and x < 2.