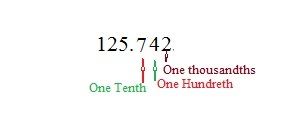
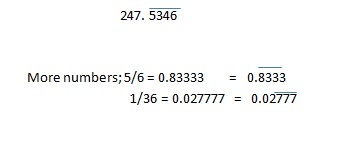To understand Decimals first we will learn the place values of numbers;
1368 . 597
8 – Unit place
6 – tens place
3 – One hundred place
1 – One Thousand Place
5 – One Tenth Place
9 – One Hundredths Place
7 – One Thousandths Place
Let us understand the decimals with following example
The number after decimal is = 742.
The place value of 7 is = 7 x 1/10
4 = 4 x 1/100
2 = 2 x 1/1000
Let us take some more example
Ex.1 – 0.568 = 5/10 + 6/100 + 8 /1000
Ex.2 – 0.0568 = 0/10 + 5/100 + 6/1000 + 8 /10000
Ex.3 – 32.459 = 3 x 10 + 2x 1 + 4/10 + 5/100 + 9/1000
Decimal To Fraction Conversion
To convert decimal to fraction just put same number of zeros after 1 in the denominator as the number of digits given after decimal .
- 0.1 = 1/10
- 6.5 = 65/10
- 2.5 = 25/10 =5/2
- 5555.55 = 555555/100 = 111111/20
- 986.2566 = 9862566/10000
Addition of Decimals;
We can understand addition of decimals like this;
Ex. 4 1256.983 + 0.25
Answer
Now Match the decimal places of numbers precisely and put a ‘0’ to match the digits ; here instead of 0.25 we can write 0.250.
Exercise;
- 0.00289 + 1.1
- 1.00005 + 0.00069
- 987625 + 0.987625
- 3658.0256 + 1 .368
- 0.011 +0.0003
Subtraction of Decimals
It is same way as normal subtraction; just take care of decimal place of the number.
Example 5 0.02 – 0.0025
Answer
Exercise;
- 5698.23 – 0.036
- 75.75 – 75
- 256896.2568 – 1245.5
- 0.35 – 0.003
- 100.245 – 12.689
Multiplication of Decimals
To multiply decimals we should multiply the same way as the whole numbers and then insert decimal according to the number of digits after decimal.
Example 6 30.05 x 1.5
Answer – There are two digits after decimal i.e. 0 and 5 in 30.05 and in 1.5 – One digit after decimal i.e. 5
So, total 2+1 =3 digits after decimal
Put the decimal before three digits from left , so the answer is 45.075.
OR
Another way to solve this sum is by converting decimals into fraction
3005/100 x 15/10 = 45075/1000 = 45.075
Exercise
- 0.01 x 0.02
- 56.023 x 1.1
- 2645.32 x 52
- 0.0005 x 0.01
- 897.87 x 45
Division of Decimals
The best way to divide one decimal with another is taking reciprocal inverse of divisor and converts both the numbers (dividend and divisor) into fraction.
Example 7 500.02 ÷ 2.02
Answer (50002/100) x (100/202)
= 247.534653465346
The decimals resulting from lengthy division either terminates or repeats itself . When the decimal values repeats without ending that time we use a bar above the repeating number; like in example 8 the decimal value 5346 repeating so we can write it like
Terminating Numbers ; 1/25 = 0.04
50/4 = 12.5
The decimals that terminates or repeats are called as Rational Numbers , While there are some numbers for which decimals do not terminate or repeat like √3 = 1.732050807568………………, π = 3.1428571………., and √7 = 2.645751…………. are known as IRRATIONAL NUMBERS.
Exercise
- 200 ÷ 1.2
- 10π ÷ 7
- 0.258 ÷ 0.36
- 782 . 26 ÷ 12.56
- √5 ÷ 5.0