Class Exercise 5

Circles Review – Fundamentals of Circles, Formulas for Circle,  Congruent Circles, Tangent to a circle, Polygon inscribed in a Circle  , Circle inscribed in a circle, Concentric Circles

Class Questions –  Exercise 1         Exercise 2      Exercise 3        Exercise 4      Exercise 5

Practice Questions – Solutions

–——————————————————————————————————–

Q. 9

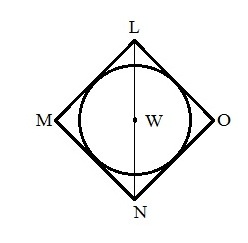
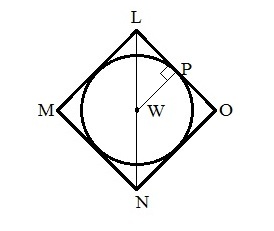
In the above figure, a circle is having center at W and radius 8. A square LMNO is circumscribed about the circle, then LN =?

                A.   12√3

                B.    10√2

                C.   16√2

                D.    4√π

                E.    18

Solution;

As LMNO is a square and circumscribed the circle. LO will be tangent to circle, if we draw a line from center of circle as WP, it will make a right angled triangle LPW.

WP = Radius of circle = 8

As LMNO is square so each side of it will be = Diameter of circle

Hence, LP = radius of circle = 8

Using Pythagorean Theorem we can easily find  the side ‘LW’ of the triangle LPW.

LW ² = LP²   +  PW²

                = 8²  +  8²

                = 64 + 64

                = 128

Taking square root both side,

LW =   8√2

LW = WN = 8√2

So,          LN = LW + WN

                                = 8√2 + 8√2

                                = 16√2

So correct answer choice is ‘C’.

—————————————————————–

Q.10        Triangle ACB is inscribed in a circle. AB is equal to diameter of circle

                                   Quantity A                                                   Quantity B

                                         Angle ‘A’                                                  Angle ‘C’

          A.  If Quantity A is greater

          B.  If Quantity B is greater

         C.  If Quantity A and Quantity B are equal

         D.  The relationship cannot be determined from given information

Solution;

As per review of circle, when any triangle is inscribed in a circle and one of the sides of the triangle is diameter of circle then that will be right angled triangle.

So, angle C = 90°, and angle A and angle B in any case have to be lesser than angle C.

Hence quantity B i.e Angle C will  be greater than quantity A.

 The correct answer choice is ‘B’.