Circles Review – Fundamentals of Circles, Formulas for Circle, Congruent Circles, Tangent to a circle, Polygon inscribed in a Circle , Circle inscribed in a circle, Concentric Circles
Class Questions – Exercise 1 Exercise 2 Exercise 3 Exercise 4 Exercise 5
Practice Questions – Solutions
–—————————————————————–
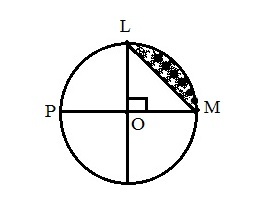
Q.7 In the following figure, the radius of the circle with center at “O” is 12 then what is the area of shaded region? Find the value.
Solution;
First find out the area of circle = π r2
= π x 122
= 144π
Next , we will calculate the area of triangle LOM,
= 1/2 x 12 x 12
= 72
Area occupied by the quarter portion of circle = area of circle/4
= 144 π/ 4
= 36π = 36 x 3.14
= 113.04
Hence area of shaded region = 113.04 – 72
= 41.04
Q.8
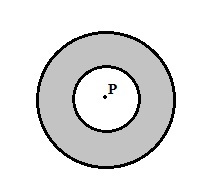
The below figure shows two concentric circles with center P. The area of outer circle is double the area of inner circle.
Quantity A Quantity B
Area of Inner circle Area of shaded region
A. If Quantity A is greater
B. If Quantity B is greater
C. If Quantity A and Quantity B are equal
D. The relationship cannot be determined from given information
Solution;
If we take radius of inner circle = r, then
Area of inner circle = π x r2
Area of Outer circle = double the inner circle
= 2 x π x r2
Area of shaded region = Area of Outer circle – Area of Inner Circle
= 2 x π x r2 – π x r2
= π x r2 = πr2
Hence the area of inner circle will be equal to area of shaded region .
The correct answer choice is C.