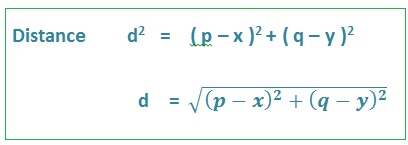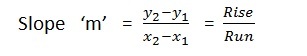Math Coordinate Geometry

     Concept of Co-ordinate Geometry

We all know about number line in which we identify the location of a number from ‘0’.

• The value of number will increase if you go right side of ‘0’. That means the point which represents a number will have a positive value.

• The value of number will decrease if you go left side of ‘0’. That means the point representing a number will have a negative value.

 

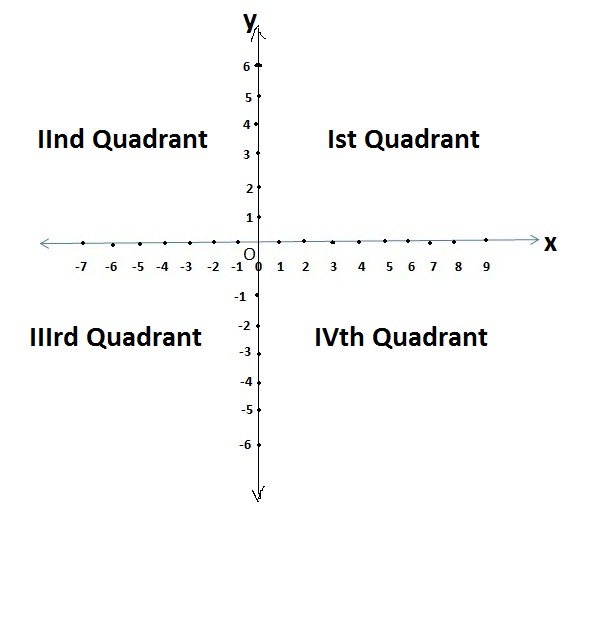
In coordinate geometry we take two number lines one is   x-axis represented as horizontal line while another is y–axis represented as a vertical line. Both the line perpendicularly intersects each other at ‘0’ and define a rectangular xy – coordinate system, generally known as xy – plane.

There are four quadrants I, II, III and IV which shows the values for coordinates of a point. The origin is at ‘O’ with the coordinates (0, 0).

Quadrant	x- coordinate	y – coordinate	Example
Ist	positive	positive	x= 2 , y = 5
IInd	negative	positive	x= -3, y =9
IIIrd	negative	negative	x= – 6, y = – 4
IVth	positive	negative	x= 1, y = – 5

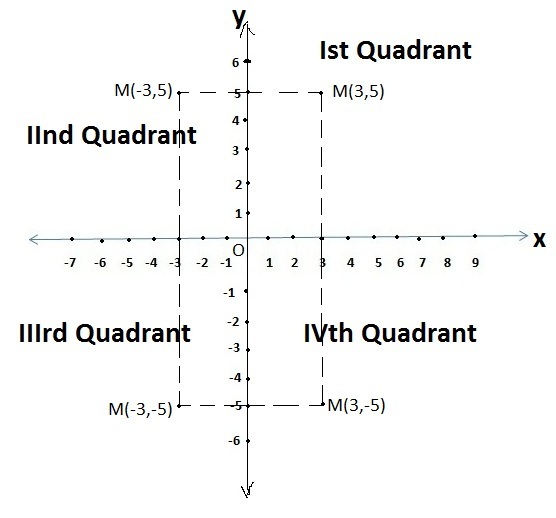
Point in any quadrant is identified with pair (x, y) of real numbers. Suppose we want to show a point ‘M’ in Ist quadrant then it can be written as M (3, 5) means there is a point whose x- coordinate is 3 and y – coordinate is 5. Similarly for other quadrants refer below figure.

Facts about Coordinate Geometry

• If x = 0, the point lies on y- axis

• If y = 0, the point lies on x- axis

• If not specified; the units of real numbers for x-axis and y-axis are same.

 Hence the xy-coordinate system is used to define the geometry of object lies in xy-plane. The objects can be rectangular , square, circle ,  polygon or any combination of  geometrical shape. The various points of the objects are defined with respect to the origin.

 

Formulas

1.Distance

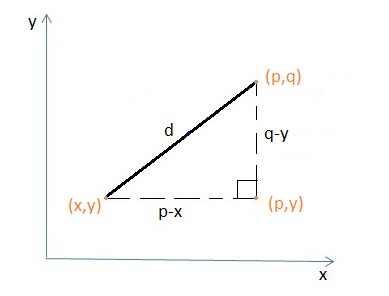
For finding distance between two points draw a right angle by adding some more lines to the line joining two points and apply Pythagorean theorem. The first point will be nearest to origin.

Let us understand with this example.

Here we are having two points M (3, 3) and N (5,-6). After adding some lines we will get a triangle LMN as shown in below figure. To find out distance between these two points apply Pythagorean Theorem for Δ LMN.

Diagonal MN = Hypotenuse, NL and LM are side arms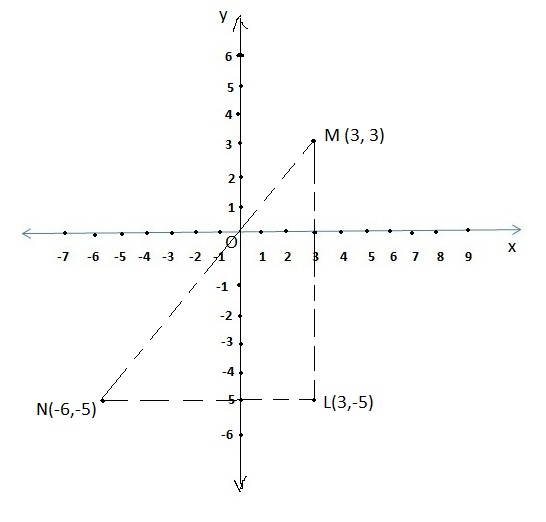

MN²   =   NL²   +   LM²

=   9² +   8²

=   81 + 64

=   145

MN = √145   = 12.04

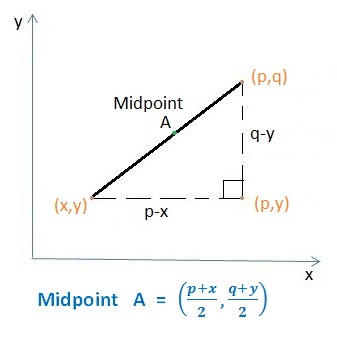
2.  Midpoint

– To find the midpoint of two points, take the average of x and y coordinates of the points.

                   

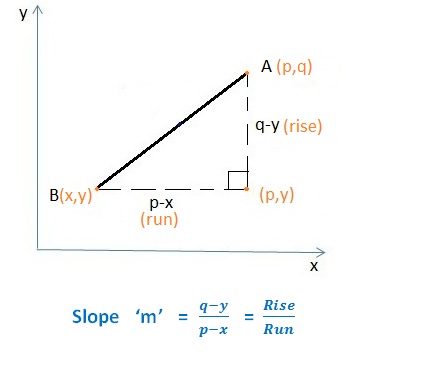
3. Slope

The slope of a line passing through two points A (p, q) and B (x, y) is the steepness of the line. It is generally represented with letter ‘m’;

• Rise is the distance that we move vertically from first value of y to second value of y.
• Run is the distance that we move horizontally from first value of x to second value of x.

Slope is always taken in terms of fraction.       Read more about Types of slope

 Graph of an Equation

The equations having two variables can be presented as graph in the coordinate plane that means one variable will be shown on x-axis and another variable will be shown on y-axis.

x- Intercept – The x-coordinates of the points at which graph intersects the x-axis.

                               At this point y-coordinate= 0

y-Intercept –  The  y-coordinates of the points at which graph intersects the y – axis.

                              At this point x-coordinate = 0

Graph of a Linear Equation – Lines

As we all know about linear equation y = mx + b, represents the straight line. Where m = slope of line,

b = y-intercept,

The slope of line passing through two points A (x₁, y₁) and B ( x₂ , y₂ )

Where   x₁   ≠   x₂

Angle of Inclination

The angle of inclination of  a   line  is  measured from  positive side of x-axis in anticlockwise direction . It is not considered after crossing the positive x-axis or not measured in clockwise direction. Thus angle of inclination may have any measure from 0º  upto  but not  including 180º .