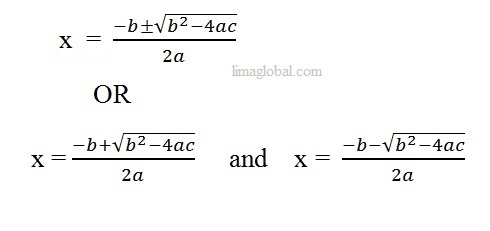Practice Examples 1 , Practice Examples 2
Quadratic Equation with one variable
The standard form of writing Quadratic equation is ax2 + bx + c = 0 , where a, b and c are real numbers and a ≠0 and x is a variable.
Whenever we square a variable there will be two possible outcomes of it; one is positive and another is negative
If x2 = 9 then x = 3 or x = -3
Similarly when x2 = 16 then x = 4 or x = – 4
Ex.1 8x2 -10x + 3 = 0
Solution
To solve the quadratic equation we factor it and these are the step we should follow to factor the equation
- Multiply the constant with x2 e. a = 8 and constant at place of ‘c’ ( ax2 + bx + c = 0 ) i.e. c = 4
- 8 x 4 = 24
- Now factor ‘24’ such that by adding or subtracting the factors you will get middle term i.e. b = -10
- So, here the factors of 24 will be -6 and – 4 by which we get multiple ; 6 x 4 = 24 and addition of (-6) + (-4) = -10
Factor the equation by taking multiples of middle term ‘10x’ as 6x and 4x
8x2 – 6x – 4x +3 = 0
2x (4x – 3) – 1(4x – 3) = 0
(4x – 3) (2x – 1) = 0
(4x-3) = 0 or (2x – 1) = 0
x = 3/4 or x = 1/2
Ex. 2 10m2 – 11m – 6 = 0
Solution; Factor the equation
10 m2 – 15 m + 4 m – 6 = 0
5m (2m – 3) + 2 (2m – 3) = 0
(2m – 3) or (5m +2) = 0
m = 3/2 or m = -2/5
Ex. 3 Convert into Quadratic Equation
(m – 5) (m + 3) = 0
Solution;
m2 + 3m – 5m – 15 = 0
m2 – 2m -15 = 0
Ex. 4 Find the solution of (x-3) (x +5) = 0
Solution; (x-3) (x + 5) = 0
(x-3) = 0 or (x+5) = 0
x= 3 or x = -5
Ex. 5 Find the solution of (2m+1) (m-8) = 0
Solution; (2m+1) (m-8) = 0
(2m +1) = 0 or (m – 8) = 0
m = -1/2 or m = 8
In general we solve quadratic equation by factorization but if the equation is not easily factored that time we find its roots using following formula;
We will get two real numbers of ‘x’ after using this formula but;
When b2-4ac ≤ 0 then we can solve like this –
1. If b2-4ac = 0 then the roots of ‘x’ will be :
x = -b/2a and we will have only one root of the equation.
2. If b2-4ac < 0 that time value of √b²-4ac will not be real and equation will not have real roots.
Ex. 6 Solve the Equation 5x2 -2x – 16 = 0
Solution; Here solving the equation with factorization is not possible we will go with roots or ‘x’
a = 5, b = -2, c = -16
>>>>>>>>>>>>>>>>NEXT PAGE