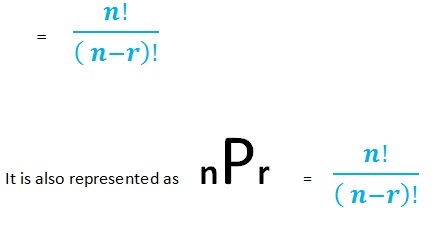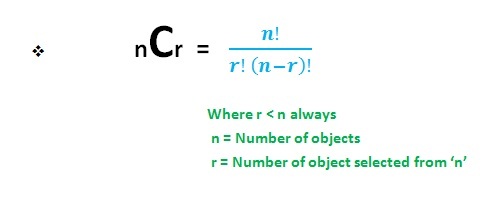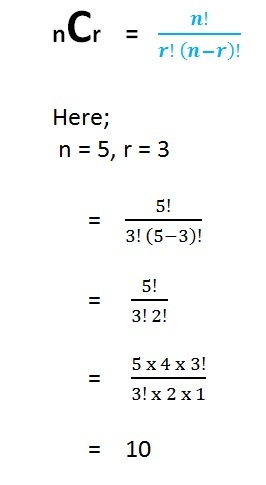Permutation and Combination

Tutorials  – Permutation and Combination

Permutation and Combination Review:  Review , Multiplication   Principle , Permutation , Factorial , Combination

Class Questions :   Exercise 1         Exercise 2         Exercise 3        Exercise 4      Exercise 5

Practice Questions :   Solutions  

_________________________________________________________________

Permutation and Combination

Permutation and Combination are Counting methods for rearrangement of “number of objects” in different ways.

Multiplication   Principle

Before we learn Permutation and Combination we need to know multiplication principle which says;

When we have to make two choices sequentially and second choice is independent of first choice then total available choices is product of first and second choices. Like If we have  ‘a’ different possibilities for first choice and ‘y’ different possibilities for second choice  then total options are available  for pair of choices  =  “a x y”.

 

Example

There are 5 pencils and 6 erasers of different colors. Lisa has to put one pencil and one eraser in a box. How many choices does she have?

Solution;

Suppose color of pencils are – red, yellow, blue, pink, purple and

Color of erasers are – green, orange, white, grey, black and golden.

So, Lisa has 5 x 6 = 30 different choices to select the pencil and eraser.

• If there are more than two independent choices, then number of choices are product of number of possibilities for every choice.

Permutation

“The meaning of word ‘Permute’ is rearrangement of objects in an order or sequence”.

Example

If we need to draw three Cartoons X, Y and Z, in how many ways Pictures of cartoons X, Y and   Z can be arranged?

Solution;

We can arrange the Pictures  in following ways;

•      X       Y       Z

•       X       Z        Y

•       Y       Z        X

•        Y      X       Z

•         Z      X       Y

•         Z      Y       X

Applying multiplication principle we can understand that making an order for arrangement, one of the three pictures must be first, one of the next two pictures must be second and last remaining must be third. Means out of three pictures first will have 3 choices, second picture will have 2 choices and third picture has only one choice for arrangement. Hence there are

3 x 2 x 1 = 6 possible ways to arrange 3 pictures in order.

When  the number of objects is more that time it is difficult to write and list all the orders possible for arrangement of those objects.

If ‘n’ objects are to be ordered from 1^st  to n^th ,  then number of ways, the objects can be ordered is for first object there are ‘n’ choices, (n – 1) choices for 2^nd object, (n – 3) choices for 3^rd object, (n – 4) choices for 4^th object and so on…………till last one choice for n^th  object.

Hence the number of ways to order the ‘n’ objects is equal to;

n (n-1)(n-2)(n-3)(n-4)(n-5)(n-6)………..(6)(5)(4)(3)(2)(1)

This is also known as number of permutations (arrangements) of ‘n’ objects. Each order is one permutation.

Factorial

When we need to count objects by multiplying;

n x (n-1) x (n-2) x (n-3) x (n-4) ……………… (4)(3)(2)(1)

So, we use a symbol “!”  –  pronounced as Factorial.

n! =   n x (n-1) x (n-2) x (n-3) x (n-4) ……………… (4)(3)(2)(1)

Like;

5! = 5 x4 x3x2x1 =120

3! = 3x2x1 = 6

1! = 1

• 0! = 1

It is necessary to know that;

• n! = n (n-1)!

              = n (n-1) (n-2)!

              = n (n-1) (n-2) (n-3)!

              = n (n-1) (n-2) (n-3) (n-4)!………and so on.

 Example:

There are 12 cars, and each of the cars will be assigned to one of 12 available parking spaces in a shopping mall. What is the number of possible arrangements for the cars in the parking space?

 Solution;

The possible number of arrangements for the car is = 12!

12!  = 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1

= 479001600

 Selecting  ‘r’ objects from given ‘n’ objects

 If we have to select ‘r’ objects from available ‘n’ objects and arrange in order from “1^st”   to  “r^th”, then there are ‘n’ choices for the first object , (n – 1) choices for the second object, (n – 2) choices for the third object,

(n – 3) choices for fourth object until we reach (n – r +1) choices for the

r^th object.

 Formula for Permutation

The number of ways to select and order ‘r’ objects from ‘n’ objects is;

 

Example

If 10 persons are watching football match and there are only 8 seats available in front row. How many ways 8 persons out of 10 can be seated, so that they can enjoy the match thoroughly?

Solution;

Using permutation formula;

n = 10, r = 8

 

 So, 1814400 choices are possible to arrange the order of seating of 8 persons.

Combination

“The combination is rearrangement of objects without considering order or sequence”.

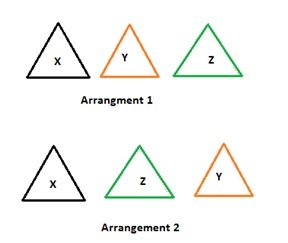
 Let us check with the following figures;

For Permutation Arrangement 1 of three triangles X, Y and Z is different than Arrangement 2.

 But in Combination   “order”     of arrangement is not required that means if we refer above figure, the arrangement 1  for three triangles X, Y and Z  is same as arrangement 2 .

 Formula for Combination

 

Fundamentally in counting methods Permutation differs from Combination is in the form of repetition of arrangement of objects.

Like in Permutation XYZ is counted as;

X       Y        Z

X       Z        Y

Z        X       Y

Z        Y        X

Y        X       Z

Y        Z        X

So we have counted same three objects X, Y and Z six times

While in Combination we will count them only once as three different objects rather than giving importance to their position of arrangement.

Permutation is useful in Bank Locker Safe, Door locks, Passwords for computer, number plate of vehicles, passport number etc.

Combination is useful in rolling dice, flipping a coin, students in a class, people visiting tourist places etc.

 

 

Example

Suppose Albert has to choose 3 fruits from a basket having  5 types of different  fruits. In how many ways he can choose the fruits?

Solution:

In this sum order of selection is not important; we need to pick 3 fruits from a basket which is having 5 different types of fruits.

To understand this sum first we take five different fruits;

   Apple, Banana, Strawberry, Mango, Kiwi

Now for choosing 3 fruits out of 5,

the possible combinations could be;

• Apple, Banana, Strawberry

• Apple, Banana, Mango

• Apple, Banana, Kiwi

• Apple, Strawberry, Kiwi

• Banana, Strawberry, Mango

• Banana, Strawberry, Kiwi

• Strawberry, Mango, Kiwi

• Strawberry, Mango, Apple

• Mango, Kiwi, Apple

• Mango, Kiwi, Banana

 

 Applying the formula for combination

So,   Albert  can choose fruits in 10 ways.