Triangle Review: Fundamentals of Triangle , Formula’s for Triangle , Types of Triangle , 45° – 45° – 90° Triangle , 30° – 60° – 90° Triangle , Congruent Triangles, Similar Triangles
Class Questions: Practice Examples 1, Practice Examples 2
Practice Questions : Exercise 1, Exercise 2, Exercise 3 , Exercise 4
—————————————————————
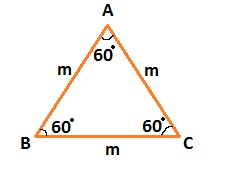
1. Equilateral Triangle
The triangle with congruent(equal) three sides as well as interior angles is know as Equilateral Triangle.
Refer the below firgure; Δ ABC is an Equilateral Triangle.
- AB = BC = AC
- ∠A = ∠ B = ∠C = 60°
2.Isosceles Triangle
The triangle with two congruent(equal) sides is known as Isosceles Triangle. The opposite angles to equal sides are also equal. They are known as base angles.
Refer the below figure; Δ PQR is a Isosceles Triangle.
- PQ = PR
- ∠ Q = ∠R
- ∠Q & ∠R are base angles.
3.Scalene Triangle
The triangle with all the three sides with different dimesions is known as Scalene Trinagle.
AB ≠ BC ≠ AC
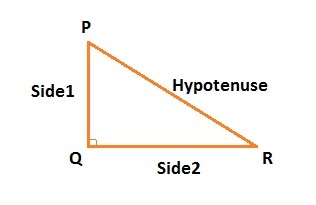
4.Right Angle Triangle
The right angle triangle or simply right triangle is any triangle with one of the angle is equal to 90°. We will use Pythagorean theorem for this type of triangle.
i.e. Hypotenuse2 = (side 1)2 + ( side 2)2 . Where hypotenuse is the longest side of triangle and being considered as diagonal to two sides of triangle.
———————————————————–
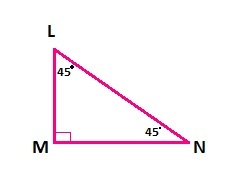
45° – 45° – 90° Triangle
Isoceles triangle with 45°, 45° and 90° angles . The speciality of this triangle is that all the three sides are in a raio of 1 : 1 : √2. ∠ L = ∠N = 45 ° and ∠M = 90° . That means if LM = MN = ‘a’ then hypotenuse LN = a√2 .
LN = Hypotenuse , LM = MN = Two Sides of triangle
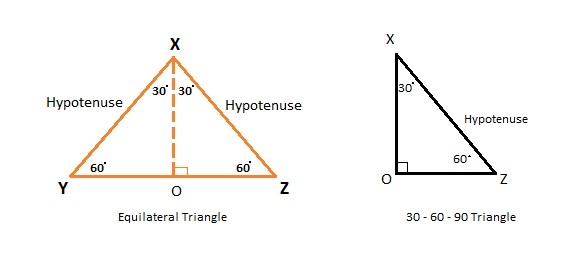
30° – 60° – 90° Triangle
An equilateral triangle with following shape. This is half of an equilateral triangle. The speciality of this triangle is that the three sides of triangel are in the ratio of 1 : √3 : 2. That means if shortest side which is opposite to smallest angle 30° , OZ = ‘a’ then OX = a √3 and XZ = 2a.
Tutorials – Triangle
Triangle Review: Fundamentals of Triangle , Formula’s for Triangle , Types of Triangle , 45° – 45° – 90° Triangle , 30° – 60° – 90° Triangle , Congruent Triangles, Similar Triangles
Class Questions : Practice Examples 1, Practice Examples 2
Practice Questions : Exercise 1, Exercise 2, Exercise 3 , Exercise 4