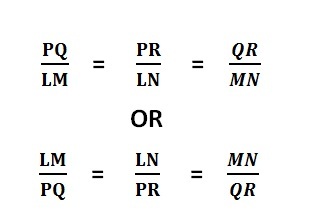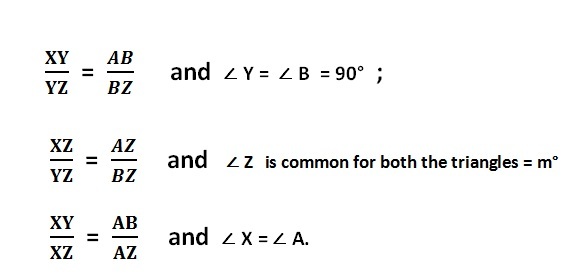Triangle Review: Fundamentals of Triangle , Formula’s for Triangle , Types of Triangle , 45° – 45° – 90° Triangle , 30° – 60° – 90° Triangle , Congruent Triangles, Similar Triangles
Class Questions : Practice Examples 1, Practice Examples 2
Practice Questions : Exercise 1, Exercise 2, Exercise 3 , Exercise 4
[embedyt] http://www.youtube.com/watch?v=GNPWD21kyZc[/embedyt]
—————————————————————–
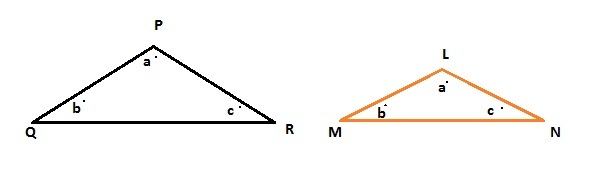
If two triangles have the same shape but not same size is known as Similar triangles.
Basically the meaning of Similar triangle is that when all the three angles of 1st triangle are congruent to corresponding all three angles of 2nd triangle then they are identified as Similar Triangles. The lengths of corresponding sides of 1st triangle are in proportion to 2nd triangle.
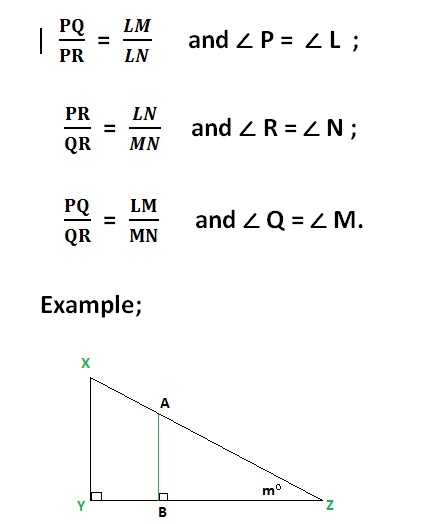
In above figure Δ PQR and Δ LMN are Similar Triangles .
Following statements are sufficient for two triangles to be similar;
a. The two triangles should have at least two corresponding congruent angles. That is in above figure for Δ PQR and Δ LMN;
if ∠ P = ∠L and ∠Q = ∠M , that means ∠R = ∠ N.
Example;
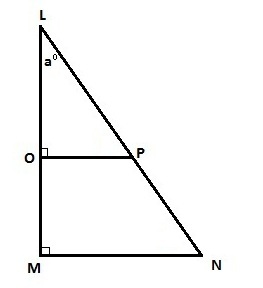
In the above figure two triangles LOP and LMN are similar triangles.
-
∠ ‘a°’ is same for both triangles.
-
∠O and ∠M are of same measure = 90°.
-
As two correspoding angles of Δ LOP and ΔLMN are same, the third correspoding angle ∠ P will be equal to ∠ N . Hence two triangles are similar triangles.
b. All the corresponding lengths of three sides of 1st triangle should have same ratio with 2nd
Both way it is right.
We can understand meaning of this equation with following example.
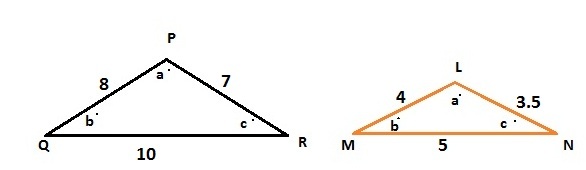
Example;
PQ = 8 ; LM = 4 which is half of PQ
QR = 10; MN = 5 which is half of QR
PR = 7 ; LN = 3.5 which is half of PR
“To understand this in simple words is that one triangle is enlarged or reduced from three sides toghether by keeping all the three angles costant”. Like If we are zooming out Δ PQR to Δ LMN or zooming in Δ LMN to Δ PQR.
c. Two sides should have lengths in same ratio and included angle between these two sides should have same measure.
In the above figure there are two triangles; Δ XYZ and Δ ABZ
Here we can go for following combinations for sides of triangles to state that Δ XYZ and Δ ABZ are similar triangles.
Triangle Review: Fundamentals of Triangle , Formula’s for Triangle , Types of Triangle , 45° – 45° – 90° Triangle , 30° – 60° – 90° Triangle , Congruent Triangles, Similar Triangles
Class Questions : Practice Examples 1, Practice Examples 2