#Geometry
Triangle
Triangle Review: Fundamentals of Triangle , Formula’s for Triangle , Types of Triangle , 45° – 45° – 90° Triangle , 30° – 60° – 90° Triangle , Congruent Triangles, Similar Triangles
Class Questions: Practice Examples 1, Practice Examples 2
Practice Questions : Exercise 1, Exercise 2, Exercise 3 , Exercise 4
Q.1 www.limaglobal.com
The two sides of the triangle are 26 and 12. What is the least possible perimeter of the triangle if, the third side is an integer?
A. 55
B. 53
C. 60
D. 52
E. 66
Solution;
As per the fundamentals of the triangle, the third side should be lesser than 26 + 12 = 38 and greater than 26 -12 = 14. The least possible value for third side will be an integer equal to 15.
The perimeter of triangle is addition of three sides = 26 + 12 + 15 = 53
The correct answer choice is ‘B’.
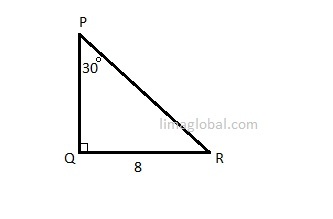
Q.2 www.limaglobal.com
What is Perimeter of following triangle PQR?
A. 8 + 8√3
B. 3√8
C. 11√3 + 3
D. 8( 3 + √3)
E. 16√3
Solution;
As we can see that this is a 30° – 60° – 90° triangle. So sides will be in the ratio of 1 : √3 : 2. As given in triangle review section the shortest side is opposite to smallest angle.
Here QR = ‘a’ = 8.
PQ = a x √3 = 8 x √3.
PR = 2 x a = 2 x 8 = 16.
Perimeter of triangle will be = PQ + QR + PR
= 8 √3 + 8 + 16
= 24 + 8√3
Or
= 8( 3 + √3 )
Hence correct answer choice is ‘D’.
Q.3 www.limaglobal.com
Triangle with vertexes A, B, C is similar to the triangle with vertexes X, Y, Z.
Quantity A Quantity B
∠ A ∠ X
A. If Quantity A is greater
B. If Quantity B is greater
C. If Quantity A and Quantity B are equal
D. The relationship cannot be determined from given information
Solution;
As per the definition and explanation given in Triangle Review section when two triangles are similar their corresponding interior angles will be same but here the figure is not given so we are not sure which way the ∠ A and ∠ X are presented in the triangles.
Like in the following figure 1st triangle with vertex A, B, C and 2nd triangle with vertex X, Y, Z. Δ ABC and Δ XYZ are similar triangles ∠A = ∠ X, Then the answer could be C.
But other way as in the below figure, 1st triangle with vertex A, B , C and 2nd triangle with vertex X, Y, Z. Δ CAB and Δ XYZ are similar triangles.
∠ A ≠ ∠ X. ∠ A is lesser than ∠ X so Quantity B will be greater, the answer could be B.
So we cannot reach to any conclusion with given information,
The correct answer choice will be ‘D’.
- Do not jump to answer but apply and answer the question on the basis of given information in relation to the question asked. And stick to that only.
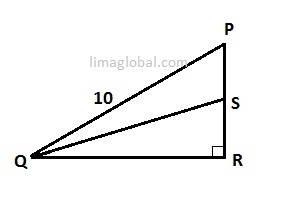
Q.4 www.limaglobal.com
In the below figure ‘S’ is the midpoint of PR. If PR = 8, what is the area of Δ PQS?
A. 48
B. 28
C. 24
D. 18
E. 12
Solution;
First we will find ‘QR’ using Pythagorean Theorem;
QR2 = QP2 – PR2
QR2 = 102 – 82
= 100 – 64
= 36
QR = 6
‘S’ is a midpoint so PS = SR = = 4
Area of Δ PQR = 1/2 x base x height
= 1/2 x 6 x 8
= 24
Area of Δ SQR = 1/2 x base x height
= 1/2 x 6 x 4
= 12
Area of Δ PQS = Area of Δ PQR – Area of Δ SQR
= 24 – 12
= 12
Another way to solve this problem is directly taking area of Δ PQS = x base x height
Here; Base = SP = 4 , Height = QR = 6
Area of Δ PQS = 1/2 x 4 x 6
= 12
So correct answer choice is ‘E’.
Q.5 www.limaglobal.com
In the following figure if BC = m, and BD = DC, then what is the length of AD?
Solution;
As we can see in the figure that Δ ABC is a 30° – 60° – 90° triangle, so the length of sides of the triangle will be in the ratio of 1:√3: 2.
BC = m so, AB = m√3 and AC = 2m
BD = DC = m/2
Now using Pythagorean Theorem;
AD2 = AB2 + BD2
So, correct answer choice is ‘B’.
>>>>>>>>>>>>>>>>>>>>NEXT PAGE
Triangle Review: Fundamentals of Triangle , Formula’s for Triangle , Types of Triangle , 45° – 45° – 90° Triangle , 30° – 60° – 90° Triangle , Congruent Triangles, Similar Triangles
Class Questions : Practice Examples 1, Practice Examples 2
Practice Questions : Exercise 1, Exercise 2, Exercise 3 , Exercise 4