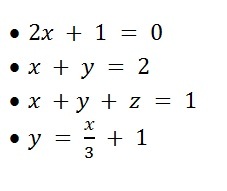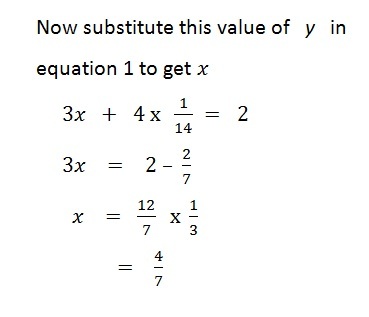Linear Equations

by

             #Algebra

Review

Practice Examples

“An algebraic equation with one or more constants and the multiplication of a number & a variable which is raised to power of 1, identified as Linear Equation”.
In mathematics linear equations are commonly written as;
lin-1
 Linear equations can have more than one constants and variables.
 Following are some of the examples to get an idea of Linear Equations.
lin-2
 Below are examples of algebraic equations which are not linear equations.
  • x2 + 2y   = 1
  • m2 + 4n + a2  = 0
  • mn – xyz + 5 = 2

Linear Equations with One Variable

As it is clear from the title itself that there is only one variable and one or more than one constants in this type of Linear Equations.

 Example

Solve the equation 6x + 5 – 8 = 6 + 4x – 4 – 3 ?
Solution;
Here it is only one variable ‘x’ and other terms are constants.
Now let us solve this equation
6x + 5 – 8 = 6 + 4x – 4 – 3
Bring all the like terms together
6x – 4x = 6 – 4 – 3 – 5 + 8
2x = 2
x = 1
  • Some time it may happen that there is no solution for linear equation like 5x – 2 = 5x + 7. The result of this equation will be
               – 2 = 7 which is not possible.
  • When value of equation on both sides of ‘=’ symbol comes same it is known as identical. That is also not a linear equation.
Like 2 (x+6) = x +x + 12. The answer to this is All Real Numbers as it is a true statement.

Linear Equations with Two Variables

 An algebraic Linear equation with two variables is being written as follows
mx + ny = p
ax + by = q

Methods for solving Linear Equations;

  1. Substitution Method
We solve one of the equations for one variable and then substitute the value in other equation to find value of second variable.

Example

Solve the following equations?

lin - 3

  1. Elimination Method

In elimination method one of the variables of both the equation made equivalent by multiplying both sides with same  number so that this variable can be eliminated by addition or subtraction of one equation with other.

Example

Solve the following equation?
 lin-4
 lin-5

Rules for Linear Equation

  • When we add or subtract the same number on both the sides the equation remains same.
  • When the equation is multiplied or divided with the same non- zero number on both sides the equation remains intact.

                                                                                                                           

………………>>>>>>>>>>>NEXT PAGE

error: